5 条题解
-
2
数据人题解,仅提供思路导引。
个人认为是一个个人差很大的题目。
算法 1
先画一棵 的二叉树,如下图所示。
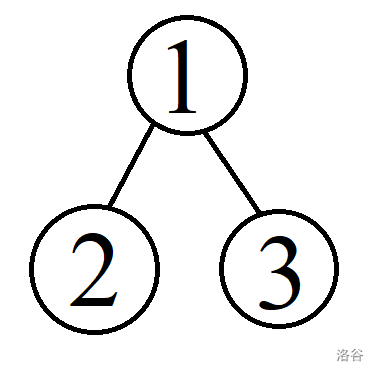
然后列一张表格,表示 的值,根据题意可以得到:
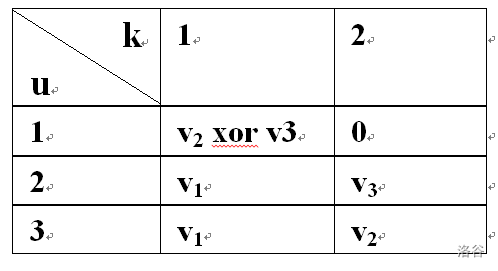
其中 是结点 的权值。
不难发现, 和 是相等的。因此只需要找到这三个点中 与其他两者不同的那个 就行,剩下两者就是所需的 。
若三个相等,则 仍然是 ,而根结点 只需要满足 即可。这个结论读者自证不难。期望得分 。
算法 2
注意到对于根节点 ,必有 。因此找到符合这个条件的结点即可。
对于根节点的权值,由于二叉树的每个结点的权值都为 ,因此只需要找到 中的非零值即可。若没有非零值,则 。
期望得分 ,结合算法 1 期望得分 。
算法 3.1
考虑对 列出 的表格。
由于只有 和 ,考虑对这张表格的每一行和每一列求异或和。
然后你会发现,第 列的异或和与根节点的 信息在数值上是能够对应上的。利用此规律就能找到根节点,期望得分 ,结合前面算法期望得分 。
算法 3.2
求出根节点之后,可以计算 的异或和,显然这个异或和是除了根节点外所有其他结点权值的异或和。
给出一个结论(from Cfz):
如果两个点的距离为奇数,那么将两个点中所有满足 为奇数的信息异或起来就能得到所有点的权值的异或和。如果两个点的距离为偶数,则异或起来会得到 。
利用这个结论就能直接求出所有结点权值的异或和。
如何发现这个结论?可以观察一下表格去凑出所有结点权值的异或和,由于直接取一列的异或和会把根节点的权值消掉,所以考虑只使用两行信息,然后就能凑出来了。
于是根节点的权值就求出来了,期望得分 。
造数据思路
确定每个结点的权值之后使用树形 dp 得到输入数据。
第一个子任务造法比较鲁莽:所有点随机权值、所有点权值为零、部分点权值为零其余随机、所有点权值为同一个值等等。造了一个 的测试点。
第二个子任务由于特殊性质,只造了这样的测试点:
所有点权值为 或同一个随机权值。然后按照数据范围卡了程序运行效率。
第三个子任务造法:
共造 组测试点。其中每一组按照程序运行效率来卡,分别有 ,,。
第一组测试点中:每一个点都是随机权值,其中随到 的概率为 ,剩下的权值等概率。
第二组测试点中:每一个点都是随机权值,其中随到 的概率为 ,剩下的权值等概率。
第三组测试点中:除第一层外,每一层随机将左半边或右半边的结点权值全部设置为 ,剩下半边随机权值。
第四组测试点中:每个点的权值很小,并且从根节点开始,对每个没有赋予权值的点进行随机游走,本次游走遍历到的点全部赋予一个相同的权值。
第五组测试点中:造法不予公开。
可能还是放过了一些错解。在此谢罪。
-
2
注意到,将所有 为 的信息异或起来可以得到所有深度为 的结点的权值的异或和 ,因为在满二叉树中,对于某个满足 的结点 ,满足 的结点 的数量为奇数,而对于某个满足 的结点 ,满足 的结点 的数量为偶数。证明显然。
于是我们可以得到,对于所有满足 的整数 ,深度为 的结点的权值的异或和,这恰恰是根结点的信息。枚举一下,找到恰好能匹配上的点即为满足条件的根结点。
再求根结点的权值。我们可以先求出所有点的权值的异或和,再异或上根结点的所有信息,得到根结点的权值。
再次注意到,如果两个点的距离为奇数,那么将两个点中所有满足 为奇数的信息异或起来就能得到所有点的权值的异或和。如果两个点的距离为偶数,则异或起来会得到 。
那我们任选一个点,枚举剩下的点,按照上述方法求出异或和。注意如果得到的全是 ,那么其实所有点的权值的异或和就是 。
于是我们就可以求出根节点的编号和根结点的权值了。
-
1
Code
#include <bits/stdc++.h> using i64 = long long; constexpr int N = 1e5 + 5, LOG = 16; int T, n, h; int f[N][LOG << 1], g[LOG]; void solve() { std::cin >> h; n = (1 << h) - 1; for (int u = 1; u <= n; u++) for (int k = 1; k <= 2 * h - 2; k++) std::cin >> f[u][k]; for (int k = 1; k < h; k++) { g[k] = 0; for (int u = 1; u <= n; u++) g[k] ^= f[u][k + 1]; } for (int u = 1; u <= n; u++) { bool ok = true; for (int k = 1; k < h; k++) ok &= (g[k] == f[u][k]); for (int k = h; k <= 2 * h - 2; k++) ok &= (f[u][k] == 0); if (ok) { int v1 = (u == 1 ? 2 : 1), all = 0; for (int v2 = 1; v2 <= n; v2++) if (v1 != v2) { all = 0; for (int k = 1; k <= 2 * h - 2; k += 2) all ^= f[v1][k] ^ f[v2][k]; if (all != 0) break; } int w = all; for (int k = 1; k < h; k++) w ^= f[u][k]; return std::cout << u << " " << w << "\n", void(); } } } int main() { std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cin >> T; while (T--) solve(); return 0; }求点赞~~~
-
1
妙妙题。
下文中令根节点的深度为 。
我们先考虑如何找出根节点 ,显然的有 $f_{r,k} = \bigoplus\limits_{u = 1}^n [\text{dep}_u = k]w_u$,我们不妨思考如何求出 $g_k = \bigoplus\limits_{u = 1}^n [\text{dep}_u = k]w_u$。
结论 1:所有 的异或和即为 。
对于每个 计算出到其距离为 的节点个数的奇偶性,从而判断其对答案有无贡献。
若 ,则在 子树内有偶数个节点到 的距离为 ,在 的子树外只有 个节点到 的距离为 (不妨假设 在根节点的左子树中,那么唯一的节点 就是根节点的右儿子),总个数为奇数,其对答案的贡献为 。
若 ,子树内仍然是有偶数个节点,子树外的部分,我们考虑 的每个祖先 (不妨设 在 的左子树内),钦定 在 的右子树内,则对于每个 ,我们都有偶数个节点 满足条件,于是其对答案的贡献为 。
若 ,子树内同理,子树外还是考虑 的每个祖先 ,对于 的祖先,我们都有偶数个满足条件的 ,对于 的祖先,我们只有一个节点(即 的右儿子)满足条件,对于 的祖先,同样也只有一个节点(即 本身)满足条件,所以总个数为偶数,对答案贡献为 。
于是,只有深度为 的节点会被计算贡献,也就证明了上述引理。
现在我们已经求出了 ,我们将其与每个节点的 逐一比对,找出根节点 (注意要判断 时, 是否全为 )。
接下来我们考虑如何求出根节点的权值,注意到我们只需求出所有节点的权值异或和即可,于是问题转化为如何求出所有节点的权值异或和。
结论 2:对于两个节点 ,若 为奇数,则所有点权的异或和即为:
$$\bigoplus\limits_{k = 1}^{2h - 2}[2\nmid k]f_{u, k}\oplus f_{v, k} $$若 为偶数,则上述式子为 。
我们要证明的就是,对于两个节点 ,若 为奇数,则到 距离为奇数的点集 和到 距离为奇数的点集 交集为空,且并集为全集。
其实已经很显然了,对于一个节点,要么它到 的距离为奇数,要么它到 的距离为奇数,容易证明这两者是对立的。
距离为偶数的证明也是类似,这里不再赘述。
于是我们只需随意固定一个点,枚举另外一个点,根据结论 2 中的式子求出异或和,若该值不为 ,则所有点权的异或和即为该值(如果得到的所有值均为 ,那么说明所有点权的异或和就是 ),然后就能求出根节点的权值 。
总的时间复杂度为 。
#include <bits/stdc++.h> using i64 = long long; constexpr int N = 1e5 + 5, LOG = 16; int T, n, h; int f[N][LOG << 1], g[LOG]; void solve() { std::cin >> h; n = (1 << h) - 1; for (int u = 1; u <= n; u++) for (int k = 1; k <= 2 * h - 2; k++) std::cin >> f[u][k]; for (int k = 1; k < h; k++) { g[k] = 0; for (int u = 1; u <= n; u++) g[k] ^= f[u][k + 1]; } for (int u = 1; u <= n; u++) { bool ok = true; for (int k = 1; k < h; k++) ok &= (g[k] == f[u][k]); for (int k = h; k <= 2 * h - 2; k++) ok &= (f[u][k] == 0); if (ok) { int v1 = (u == 1 ? 2 : 1), all = 0; for (int v2 = 1; v2 <= n; v2++) if (v1 != v2) { all = 0; for (int k = 1; k <= 2 * h - 2; k += 2) all ^= f[v1][k] ^ f[v2][k]; if (all != 0) break; } int w = all; for (int k = 1; k < h; k++) w ^= f[u][k]; return std::cout << u << " " << w << "\n", void(); } } } int main() { std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cin >> T; while (T--) solve(); return 0; }
- 1
信息
- ID
- 31
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 10
- 标签
- 递交数
- 253
- 已通过
- 24
- 上传者