1 条题解
-
0
「ALFR Round 5」地铁
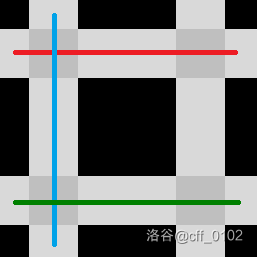
- 如图,首先,当 时,我们考虑每一行或每一列都只有一条地铁线,如果 那就就选 条,反之则选 条。这样可以使地铁线覆盖范围更广,同时也能使地铁线路最少。
- 但是铁路还要满足无论从哪个地铁站出发乘坐地铁,经过若干次换乘(可以不换乘),都一定可以到达其它所有地铁站。所以必定有一条线路分别和上述的 条线路至少有一个交点。所以答案为 。
- 当 或 时,此时只需要一条长为 或 的铁路线来使其覆盖全部即可。
- 故答案 为:
#include<bits/stdc++.h> using namespace std; typedef long long ll; ll n,m,t; int main(){ cin>>t; while(t--){ cin>>n>>m; if(n==1||m==1) cout<<1<<endl; else cout<<min(n,m)+1<<endl; } }
- 1
信息
- ID
- 141
- 时间
- 3000ms
- 内存
- 512MiB
- 难度
- 1
- 标签
- 递交数
- 150
- 已通过
- 103
- 上传者