2 条题解
-
1
666 这场比赛怎么全是 DP。题意
连续 个下标 ,最开始你在下标 ,每次可以从 走到 和 ,或者走到 的约数下标(这是两种不同的走法),每个下标只能走一次,问你有多少种从 走到 的走法(不能走出 到 的范围)。
思考过程
如果只有向一边走的情况,那么这个题很容易做,但是这里多出来一种向回走的情况,这就不太好考虑了。
但是我们可以发现,向回走一定是只能一格一格的走,并且一定存在于原来某次跳约数的中间未被访问的部分。
比如下图中从 跳到 (跳约数),这样的话, 到 的下标都没有被跳过,因此完全可以考虑这个时候从 往回一格一格跳,比如考虑跳到 ,那么此时所有能够跳到 的方案,通过 一定能够跳到 ,所以此时可以让 累加上跳到 的方案,注意不是加 的, 中包含有其他的方案,与我们现在讨论的不一致。
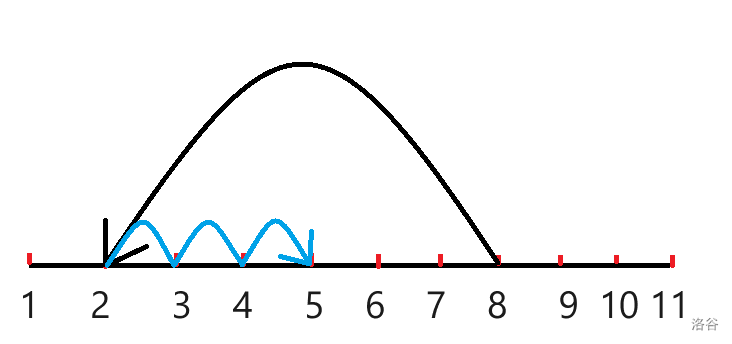
但是直接加上 的就好了吗?实际上还存在一类问题。
绿色和红色是曾今走到 的一种决策,这一决策经过了 ,而如今我们在对 进行决策时,却没有考虑到 已经被先前的某些方案所覆盖(已经被走过了),所以我们必须记录一下,点 是从前面哪个点往后走到的,比如这里 是从 走到的,所以后来我们在考虑蓝色路径时(对 的决策),只能让 累加上从 走到 (这个东西就是个后缀和嘛),或者从 后面来到 的情况的方案数。
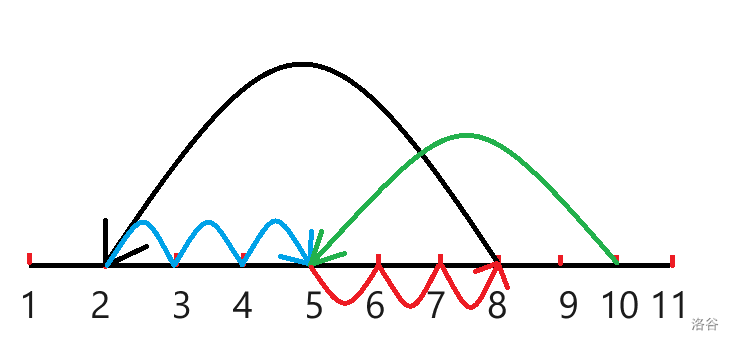
所以接下来思路就很明确了:
定义状态 表示从 向后走走到的 的方案数,这里我为了好统计,将 的状态特殊定义为从 后面走到 的方案数。
对于向前一格的情况:
对于从 跳约数来到 的情况:( 是 的约数)
接下来着重看一下往回跳的情况
下面是 的情况,我们考虑 通过约数的跳法来到 ,此时我们在 到 中枚举 ,此时将 累加上 从 跳过来的方案数:对于 有 (从后面来到 的方案数根据定义统计在 中,被正常累计在 上)。
我们是在对第 中的第二维进行后缀和,第二维就是下图中的 (对于每次枚举的 ,只需要修改 和 ),所以对于每个 计算完后,再刷一遍 的后缀和就好了。具体的,每次关于 的计算结束后,枚举 ,令
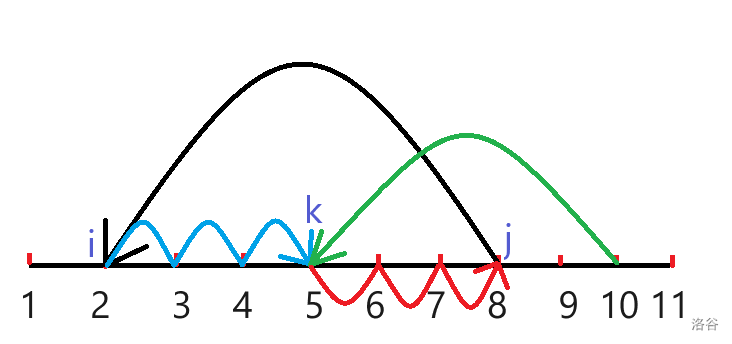
时间复杂度
第一层循环一个 ,第二层循环 的倍数 (不包括 ),第三层循环 到 的所有数
第一层可以看成 ,因为再往上就不会有 的倍数了(因为倍数都超过 )。
接下来第二层和第三层是一个等差数列求和,公差为 。对于一个 ,需要计算 $[i,2\times i],[i,3\times i],[i,4\times i],...,[i,n]$ 这些区间(每个区间长度比前一个多 ,共有 个区间),计算次数就是 $(2\times i-i)+(3\times i-i)+(4\times i-i)+...+(n-i)$,这里直接把 看成 就好。
$i+2\times i+3\times i+...+n=\frac{n-i}{i}\times \frac{(n+i)}{2}$, 是项数。
把 估大成 ,把 估大成 。
得到 $\frac{n}{i}\times\frac{2\times n}{2}=\frac{2\times n^2}{2\times i}=\frac{n^2}{i}$,再把 带入得到 $\displaystyle\sum_{i=1}^{\frac{n}{2}}\frac{n^2}{i}=n\times \displaystyle\sum_{i=1}^{\frac{n}{2}} \frac{n}{i}=n^2\times\ln(n)$,ok拿下。
#include<bits/stdc++.h> using namespace std ; const int Max = 5e3 + 10 ; vector < int > Start[Max] , Prinm[Max] ; int g[Max][Max] ; int f[Max][Max] ; int n , p ; int main( ) { scanf("%d%d" , &n , &p ) ; // 边界情况特殊处理 f[n + 1][n + 1] = 1 ; for(int i = n ; i >= 1 ; i -- ) { // i 从 i+1 走来 // 所以对 f[i][i] 修改即可 f[i][i] = ( f[i][i] + f[i + 1][i + 1] ) % p ; for(int l = 2 * i ; l <= n ; l += i ) { // i 从 l 跳来,这里注意只有 l 是从 i+1,i+2,...,l 跳过来的方案需要被累计 f[i][i] = ( f[i][i] + f[l][i + 1] ) % p ; for(int k = i + 1 ; k <= l - 1 ; k ++ ) { // l 从 k+1,k+2,...,l 跳过来 // k 从 i 跳过来 f[k][i] = ( f[k][i] + f[l][k + 1] ) % p ; } } // 每次 i 计算完,救刷新一下后缀和 for(int l = 1 ; l <= n ; l ++ ) f[l][i] = ( f[l][i] + f[l][i + 1] ) % p ; } // 答案就是从 1 后面跳过来 printf("%d\n" , f[1][1] ) ; return false ; } -
-1
从点 开始,只有两种跳法:跳到 处,或者跳到 的因子 处. 跳到 处后等同于从 处开始,但跳到 和从 开始有一定区别,因为跳完后还可以往前跳(只要不超过 即可).

(上图黑线表示第一步、蓝线表示第二步,直线表示从 跳到 的类型,曲线从 跳到 的因子的类型.)
我们用 表示从 出发到 ,且经过的点在 范围内的方案数,我们要求的答案即为 . 根据前面的分析,可以得到:
那么对于 的 怎么求呢?首先根据定义 的方案对 有贡献.
如果我们要到达 点,必须是刚开始就从 向前跳到 ,到达 点后,不能再到 或者 ,只能跳到 的因子处离开,且这个因子必须小于 .
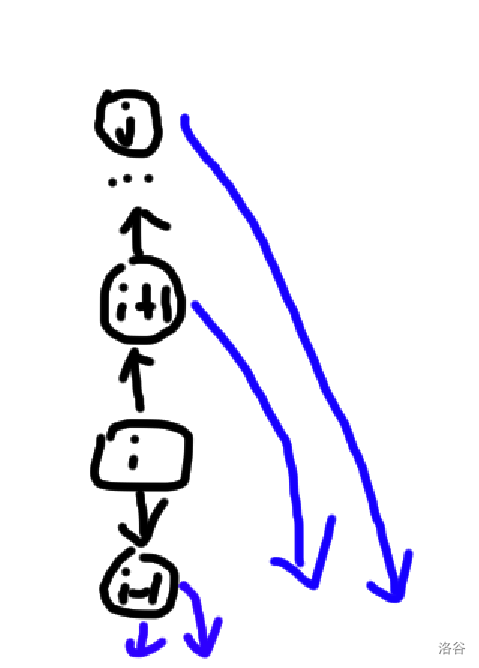
可以得到:
观察到我们推的两个式子形式相似,可以放在一个循环中,动态规划的边界即为 .
对于每个数,我们可以提前预处理因子,算法的时间复杂度为 ,优化一下常数,把对 取模改成减去 即可通过.
代码:
#include <iostream> #include <vector> const int MAXN = 5005; using namespace std; int n; long long f[MAXN][MAXN], mod; vector<int> d[MAXN]; int main() { cin >> n >> mod; for (int i = 1; i <= n; ++i) f[1][i] = 1; for (int i = 1; i <= n; ++i) { for (int j = 1; j * j <= i; ++j) { if (i % j == 0) { d[i].push_back(j); if (i / j != j) d[i].push_back(i / j); } } } for (int i = 2; i <= n; ++i) { f[i][i] = f[i - 1][i - 1]; for (int j = i; j <= n; ++j) { f[i][j] += f[i][j - 1]; for (int k : d[j]) { if (k < i) { f[i][j] += f[k][i - 1]; if (f[i][j] > mod) f[i][j] -= mod; } } } } cout << f[n][n] % mod << endl; return 0; }
- 1
信息
- ID
- 19
- 时间
- 2000ms
- 内存
- 512MiB
- 难度
- 6
- 标签
- 递交数
- 237
- 已通过
- 48
- 上传者