7 条题解
-
2
我们可以从前往后模拟一遍,寻找思路。
这里使用样例三进行分析。
输入:
1 1 45 14。 输出:3。模拟过程:
第一次:到第三项时,删除 ,将 改为 ;
第二次:删除这个 ,将 改为 ;
第三次:删除 ,把 改为 ,就结束操作了。
那么,我们发现,这是一个线性进行的过程,这让我想起了一个数据结构——队列。我们可以用队列来模拟这个过程。
我的思路:从第一项开始,将暂时删不掉的项入队(由于删不掉的必然与前一项相等,所以能保留在队列中的所有项都一定相等),接着当队尾遇到能被删除的项(就是与队尾不相等的项)时,立刻开始执行操作。
因为之前能保留在队列中的所有项都相等,那么当我们追求最优,修改队尾的值时,队列中的所有项都可以被修改,那么此时还会有一个被修改的项存在队列里。我们不必关心此时它的值,因为它可以修改成任意整数,这就意味着从它开始,这个队列就只可能存在一个项,再往后模拟时,就只要一次一次加操作数就行了。
因为它是任意的,所以之后的项肯定都会被其删掉。这道题就这样解决掉了。
由于每一项至多入队一次,所以时间复杂度为 ,完全足以过掉这道题。详情见代码注释。
接下来是代码时间(代码比较拙劣,见谅)。
#include<bits/stdc++.h> #define maxn 100005 using namespace std; int n, ans; //ans计算操作数 int a[maxn]; queue<int> q; int main() { ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); cin>>n; bool ok=1; for(int i=1;i<=n;i++) { cin>>a[i]; if(i!=1&&a[i]!=a[i-1])ok=0; } if(ok) {//如果每一项都相等,就操作不了,输出0,对应第2个子任务 cout<<0;return 0; } if(n<=2) {//一个小特判,对应第一个子任务 if(n==1) cout<<0; //只有一项无法操作,输出0 else cout<<1; //此时两项必然不相等,可以操作一次 return 0; } bool flag=0; //存储队首是否参与操作 for(int i=1;i<=n;i++) { if(q.empty())q.push(a[i]);//如果队列为空就加入 else if(a[i]==q.front()&&!flag)q.push(a[i]); //如果和队首相等就删不了,要加入,但是如果队首之前参与过操作,这一项也得删除 else { ans++; //要删,操作数加1 while(q.size()>1){ //一次性操作到只剩一个 flag=1; q.pop(); ans++; } } } cout<<ans; //输出,一次过 return 0; }写作不易,还请各位点赞支持一下。
如有不足,还请指出,感谢各位观看。
-
0
题目大意
给一个长度为 的序列 ,每次操作可以选择一个整数 ,在 的情况下删除 并修改 ,求共可以进行几次操作。
思路
通过观察样例可以发现,当序列中的每一项都相等时,是无法进行操作的,因为没有任意 满足 ,此时答案为0。
此外,只要有一个与其它项不同的项,那么我们可以操作到序列中仅有一个项,在这里放个图: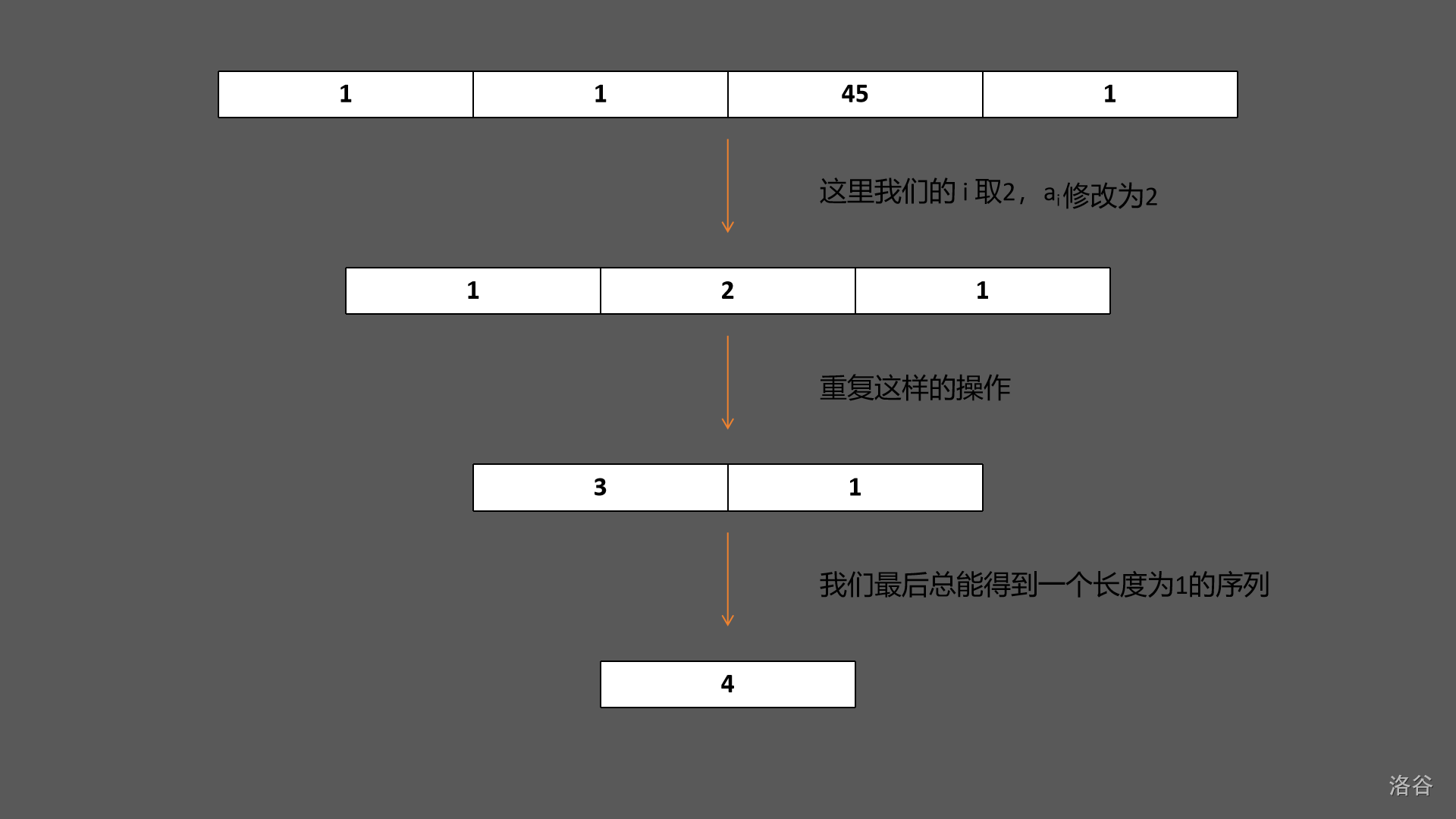
可见其中 个数都被删除了,则结果为 。
那么我们可以愉快地写代码啦!代码实现
#include<bits/stdc++.h> using namespace std; int main(void) { int n,a[100005]= {0},b,flag=1; //开的空间比数据范围大5是个好习惯 cin>>n>>a[1],b=a[1]; for(int i=2; i<=n; i++) { cin>>a[i]; if(a[i]!=b)flag=0; } if(flag)cout<<0; else cout<<n-1; return 0; } -
-1
给你一个序列 。你可以对这个序列进行若干次操作。
设一次操作前序列长度为 ,那么这次操作你可以选择一个整数 使得 且 ,删除 并把 的值设成任意整数。
求你最多能进行多少次操作。
假设序列分为 段,第 段的数均为 ,第 段的长度为 。
此处
- ;
- 对于 ,。
那么序列 可以表示为这样:
$$a=\underbrace{t_1,t_1,\cdots,t_1}_{l_1\,\text{个}},\cdots\underbrace{t_x,t_x,\cdots,t_x}_{l_x\,\text{个}} $$
容易发现,如果 ,即 数组全部都是一个数的话,那么是无法操作的,输出 即可。
否则,序列至少存在 和 。
此时 可以与第 个数 消掉,得到一个数 。
由于可以将 的值设为任意整数,那么 ,使得对于 ,有 。
那么可以用 消掉第 个数,此时序列可以变为:
$$a=\underbrace{t_1,t_1,\cdots,t_1}_{l_1-1\,\text{个}},p $$由于 ,所以从后向前消,最后序列可以变为
容易发现,此时序列操作了 次。
综上所述,分类讨论:
- 如果 由一个数构成,输出 ;
- 反之,输出 。
#include <bits/stdc++.h> const int N = 1e5 + 10; int n, a[N]; int main() { std::cin.tie(0)->sync_with_stdio(0); std::cin >> n; for (int i = 1; i <= n; ++i) std::cin >> a[i]; for (int i = 2; i <= n; ++i) { if (a[i] != a[i - 1]) { // 发现不同的数字 std::cout << n - 1 << std::endl; return 0; } } std::cout << 0 << std::endl; // 全部都相同 return 0; } -
-2
J2B 题解
部分分 Subtask :因为数字都相同,没有可以进行的操作,输出 即可。
接下来思考满分做法。因为数字不同时一定有至少一次可操作的,可以先操作这个数,然后将前面的数修改为与前后的数都不相同的任意一个数,一直操作下去,最终数列一定只会余下一个数。此时共操作 次。
代码:
#include<iostream> using namespace std; int a[100001]; int main() { int n; cin>>n>>a[1]; for(int i=2;i<=n;i++) { cin>>a[i]; if(a[i]!=a[i-1])return cout<<n-1,0; } cout<<0; return 0; } -
-2
Turtle and Sequences题解
思路
先说一个错误的思路
我一开始做的思路有点问题,把这道题当成了类似去重的题。 就是在输入的时候,如果输入的数与上一个数不同,就读入,否则跳过。最后数组内数的多少就是答案。 写完调试了老半天,好不容易把样例调试对了,交上去喜提53分。
后来重新读了题,才发现貌似理解错了题目的意思。举一个例子。
以下面样例为例:
7 1 3 3 3 3 2 1如果按照原来的思路,就会得到 的结果。但实际上,答案应该是 。具体过程如下。 由于可以将值设成任意整数,那我们设 为一个很大的整数。
步骤见下:
操作次数 数组 1 1 3 3 3 3 k 2 1 3 3 3 k+1 3 1 3 3 k+2 4 1 3 k+3 5 1 k+4 6 k+5当然步骤不是唯一的。
由此可见,只要保证操作结束后得到的数与前面不同,就可以继续进行操作。操作了 次。
特殊情况
当所有数都一样时,答案为 ,易证。
Code
#include<bits/stdc++.h> using namespace std; typedef long long ll; int n,flag,a[100005]; int main() { ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin>>n>>a[1]; for(int i=2;i<=n;i++) { cin>>a[i]; if(a[i-1]!=a[i]) flag=1; } if(flag) cout<<n-1; else cout<<0; return 0; }写篇题解不容易,求点赞。不足请指出。
-
-2
题解 Turtle and Sequences
思路
可以用一个测试用例来找规律。 比如说有这几个数:
1 1 4 5 1 4
可以发现,只要遇到两个不同的数 和 , 可以保证操作结束后得到的新数跟所有的数不一样。 所以又可以跟其他的数进行操作了。所以只有这两个情况了:
- 有一对不相同:总共 次。
- 都相同:总共执行了 次。
解题方法
只要遇到两个数不同,输出 ,否则输出 。
复杂度为。Code
#include <bits/stdc++.h> using namespace std; int a[100005]; int main(){ int n; cin >> n; for (int i = 1; i <= n; i++) { cin >> a[i]; } int cnt = 0; for (int i = n; i > 1; i--) { if(a[i] != a[i - 1]) { cnt = n - 1; break; } } cout << cnt << "\n"; return 0; } -
-3
标题
思路
解题方法
复杂度
时间复杂度:
添加时间复杂度, 示例:
空间复杂度:
添加空间复杂度, 示例:
Code
#include<bits/stdc++.h> #define maxn 100005 using namespace std;
int n, ans; //ans计算操作数 int a[maxn]; queue q;
int main() { ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); cin>>n; bool ok=1; for(int i=1;i<=n;i++) { cin>>a[i]; if(i!=1&&a[i]!=a[i-1])ok=0; } if(ok) {//如果每一项都相等,就操作不了,输出0,对应第2个子任务 cout<<0;return 0; } if(n<=2) {//一个小特判,对应第一个子任务 if(n==1) cout<<0; //只有一项无法操作,输出0 else cout<<1; //此时两项必然不相等,可以操作一次 return 0; } bool flag=0; //存储队首是否参与操作 for(int i=1;i<=n;i++) { if(q.empty())q.push(a[i]);//如果队列为空就加入 else if(a[i]==q.front()&&!flag)q.push(a[i]); //如果和队首相等就删不了,要加入,但是如果队首之前参与过操作,这一项也得删除 else { ans++; //要删,操作数加1 while(q.size()>1){ //一次性操作到只剩一个 flag=1;
q.pop(); ans++; } } } cout<<ans; //输出,一次过 return 0; }
- 1
信息
- ID
- 21
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 2
- 标签
- 递交数
- 1534
- 已通过
- 401
- 上传者