完美二叉树

测试点 $1$

总共有 $3$ 个节点，直接分讨。

测试点 $2 \sim 3$

注意到 $2^{10}=1024$，树上的节点至多 $1023$ 个。

建树，对于每个询问暴力遍历整棵树并标记哪些节点和 $x$ 的距离不超过 $k$，哪些节点和 $y$ 的距离不超过 $k$，然后枚举节点计算答案。

时间复杂度 $O(2^nm)$。

测试点 $4 \sim 5$

树上节点至多有 $2^{18}-1=262143$ 个。

注意到 $k_i \leq 5$，所以和某个节点的距离不超过 $k_i$ 的节点不会太多。

具体有多少呢？首先对于给定节点 $x$，它自己肯定满足要求（距离为 $0$），如果 $x$ 既不是叶子节点也不是根节点，它就一定有 $3$ 个相邻节点（距离为 $1$），这 $3$ 个相邻节点既不是叶子节点也不是根节点的话，它们每个节点就也有 $3$ 个相邻节点，排除掉 $x$ 之后它们每个节点都能贡献 $2$ 个新的节点（距离为 $2$）...

可以得到满足条件的节点数量不超过 $1+3+3 \times 2+3 \times 2^2+3 \times 2^3+3 \times 2^4=94$ 个，询问时暴力遍历的效率可以接受。

对于第 $i$ 次询问，先从节点 $x_i$ 开始遍历，标记所有与 $x_i$ 距离不超过 $k_i$ 的节点；然后从节点 $y_i$ 开始遍历，遇到有标记的节点就将其计入答案。注意清空标记时应当只清空被标记的节点，否则时间复杂度可能退化。笔者的做法是再从 $x_i$ 遍历一次并取消被遍历到的节点的标记。

这里认为回答一次询问的时间复杂度为 $O(1)$，总体时间复杂度 $O(2^n+m)$。

这个做法能通过测试点 $1 \sim 5$ 并获得 $50$ 分，注意答案可能超出 int 范围。

#include<bits/stdc++.h>
using namespace std;
int n,m,lim,w[300'000];
vector<int> v[300'000];
bool on[300'000];
long long ans;
void dfs(int x,int las,int step,int uim,function<void(int)> fun){
    fun(x);
    if(step<uim) for(int i:v[x]) if(i!=las) dfs(i,x,step+1,uim,fun);
}
long long query(int x,int y,int k){
    ans=0ll;
    dfs(x,0,0,k,[&](int x)->void{on[x]=1;});
    dfs(y,0,0,k,[&](int x)->void{ans+=on[x]*w[x];});
    dfs(x,0,0,k,[&](int x)->void{on[x]=0;});
    return ans;
}
int main(){
    ios::sync_with_stdio(0);
    cin>>n>>m,lim=(1<<n)-1;
    for(int i=1;i<=lim;i++) cin>>w[i];
    for(int i=2;i<=lim;i++) v[i].push_back(i/2),v[i/2].push_back(i);
    for(int i=1;i<=m;i++){
        static int x,y,k;
        cin>>x>>y>>k;
        cout<<query(x,y,k)<<'\n';
    }
    return 0;
}

测试点 $6 \sim 7$

现在尝试将问题转化，举个例子：询问和节点 $8,14$ 的距离都不超过 $5$ 的节点权值和。

这等价于询问所有和节点 $1$ 的距离不超过 $2$ 的节点权值和。

为啥？因为节点 $1$ 到节点 $8,14$ 的距离相等，是路径中点。对于节点 $2$ 子树中的节点，它们与节点 $14$ 的距离肯定比与节点 $8$ 的距离大，所以只要这些节点与节点 $14$ 的距离符合要求，它们就一定符合要求。节点 $3$ 子树中的节点同理，只要它们与节点 $8$ 的距离符合要求，也就一定符合要求。

又因为节点 $1$ 到节点 $8,14$ 的距离相等（$3$），所以只用计算和节点 $1$ 的距离不超过 $5-3=2$ 的节点权值和。

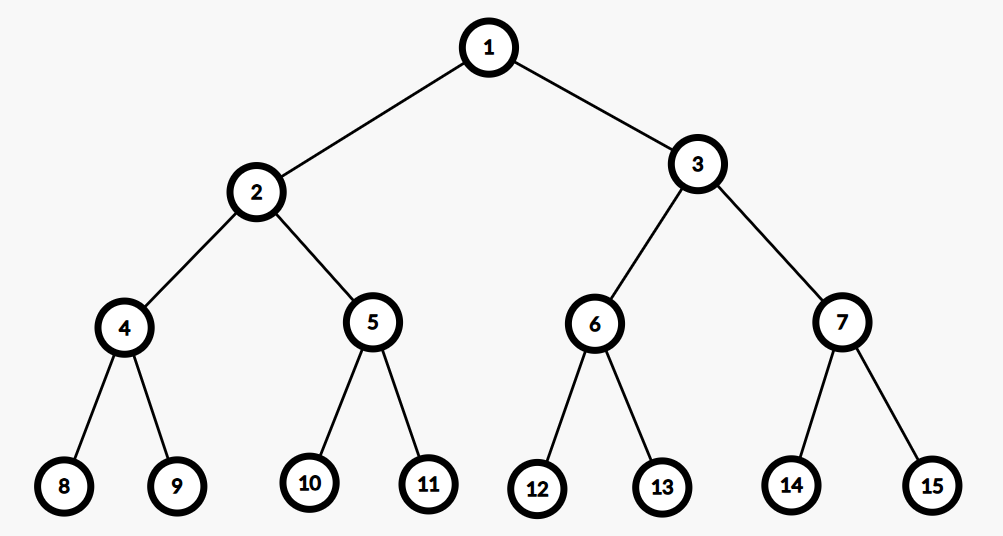
再来一个例子：询问和节点 $5,13$ 的距离都不超过 $4$ 的节点权值和。

这等价于询问所有和节点 $1,3$ 形成的连通块的距离不超过 $1$ 的节点权值和。转化方式同上，由于路径上的节点有偶数个计算过程会复杂一些。

现在尝试利用 $w_i=1$ 的条件，注意到给定的树是一棵完美二叉树，所以当节点 $x$ 的子树中存在与其距离为 $k$ 的节点时，它子树内与节点 $x$ 距离不超过 $k$ 的节点权值和为 $2^k-1$。

又因为完美二叉树的性质很好，从任意节点向上枚举到根节点的时间复杂度为 $O(n)$，可以一边向上枚举一边计算答案，具体实现见文末代码。

时间复杂度 $O(2^n+nm)$。

另外由于 $w_i=1$，本质不同的询问只有 $O(n^3)$ 个，可能存在其他的做法。

测试点 $8 \sim 10$

沿用上一个做法，预处理节点 $x$ 的子树中与其距离不超过 $k$ 的节点权值和。因为完美二叉树的性质很好甚至不用把树建出来。计算答案时很可能需要当前节点兄弟的信息，因为完美二叉树的性质，节点 $x$ 的兄弟就是 $x \oplus 1$（$\oplus$ 表示异或），这是容易的。

时间复杂度 $O(n2^n+nm)$。

#include<bits/stdc++.h>
using namespace std;
long long s[20][300'000];
int n,m,lim;
void dfs(int x){//预处理节点子树权值和
    if(x*2>lim){
        for(int i=1;i<=n;i++) s[i][x]=s[0][x];
        return;
    }
    dfs(x*2),dfs(x*2+1);
    for(int i=1;i<=n;i++) s[i][x]=s[0][x]+s[i-1][x*2]+s[i-1][x*2+1];
}
long long query(int x,int y,int k){
    static int xi,yi,mid,cnt[2],a[2][40];
    static long long ret;
    xi=0,yi=1,cnt[0]=0,cnt[1]=0;
    while(x!=y){
        if(x<y) swap(x,y),swap(xi,yi);
        a[xi][++cnt[xi]]=x,x/=2;
    }
    a[xi][++cnt[xi]]=x;
    for(int i=cnt[yi];i>=1;i--) a[xi][++cnt[xi]]=a[yi][i];
    k-=cnt[xi]/2;
    if(k<0) return 0ll;
    if(cnt[xi]%2==1){//存在唯一的路径中点
        mid=a[xi][cnt[xi]/2+1];
        ret=s[min(k,n)][mid];
    }
    else{//不存在路径中点需要处理的东西更多
        mid=max(a[xi][cnt[xi]/2],a[xi][cnt[xi]/2+1]);
        ret=s[min(k,n)][mid];
        if(k>=1) ret+=s[min(k-1,n)][mid^1];
        mid/=2,ret+=s[0][mid];
    }
    for(int i=1;i<=k&&mid!=0;i++){//向上枚举
        if(k-i>=1) ret+=s[min(k-i-1,n)][mid^1];
        mid/=2,ret+=s[0][mid];
    }
    return ret;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>n>>m,lim=(1<<n)-1;
    for(int i=1;i<=lim;i++) cin>>s[0][i];
    dfs(1);
    for(int i=1;i<=m;i++){
        static int x,y,k;
        cin>>x>>y>>k;
        cout<<query(x,y,k)<<'\n';
    }
    return 0;
}

标:114514