5 条题解
-
2
数据人题解,仅提供思路导引。
个人认为是一个个人差很大的题目。
算法 1
先画一棵 的二叉树,如下图所示。
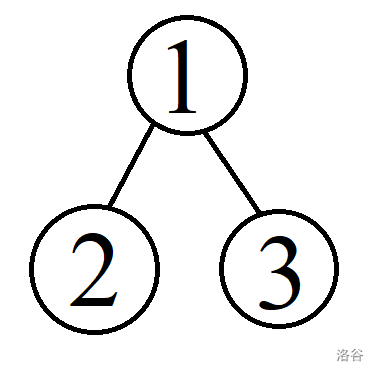
然后列一张表格,表示 的值,根据题意可以得到:
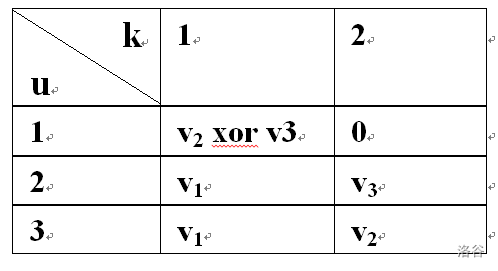
其中 是结点 的权值。
不难发现, 和 是相等的。因此只需要找到这三个点中 与其他两者不同的那个 就行,剩下两者就是所需的 。
若三个相等,则 仍然是 ,而根结点 只需要满足 即可。这个结论读者自证不难。期望得分 。
算法 2
注意到对于根节点 ,必有 。因此找到符合这个条件的结点即可。
对于根节点的权值,由于二叉树的每个结点的权值都为 ,因此只需要找到 中的非零值即可。若没有非零值,则 。
期望得分 ,结合算法 1 期望得分 。
算法 3.1
考虑对 列出 的表格。
由于只有 和 ,考虑对这张表格的每一行和每一列求异或和。
然后你会发现,第 列的异或和与根节点的 信息在数值上是能够对应上的。利用此规律就能找到根节点,期望得分 ,结合前面算法期望得分 。
算法 3.2
求出根节点之后,可以计算 的异或和,显然这个异或和是除了根节点外所有其他结点权值的异或和。
给出一个结论(from Cfz):
如果两个点的距离为奇数,那么将两个点中所有满足 为奇数的信息异或起来就能得到所有点的权值的异或和。如果两个点的距离为偶数,则异或起来会得到 。
利用这个结论就能直接求出所有结点权值的异或和。
如何发现这个结论?可以观察一下表格去凑出所有结点权值的异或和,由于直接取一列的异或和会把根节点的权值消掉,所以考虑只使用两行信息,然后就能凑出来了。
于是根节点的权值就求出来了,期望得分 。
造数据思路
确定每个结点的权值之后使用树形 dp 得到输入数据。
第一个子任务造法比较鲁莽:所有点随机权值、所有点权值为零、部分点权值为零其余随机、所有点权值为同一个值等等。造了一个 的测试点。
第二个子任务由于特殊性质,只造了这样的测试点:
所有点权值为 或同一个随机权值。然后按照数据范围卡了程序运行效率。
第三个子任务造法:
共造 组测试点。其中每一组按照程序运行效率来卡,分别有 ,,。
第一组测试点中:每一个点都是随机权值,其中随到 的概率为 ,剩下的权值等概率。
第二组测试点中:每一个点都是随机权值,其中随到 的概率为 ,剩下的权值等概率。
第三组测试点中:除第一层外,每一层随机将左半边或右半边的结点权值全部设置为 ,剩下半边随机权值。
第四组测试点中:每个点的权值很小,并且从根节点开始,对每个没有赋予权值的点进行随机游走,本次游走遍历到的点全部赋予一个相同的权值。
第五组测试点中:造法不予公开。
可能还是放过了一些错解。在此谢罪。
信息
- ID
- 31
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 10
- 标签
- 递交数
- 253
- 已通过
- 24
- 上传者