2 条题解
-
-1
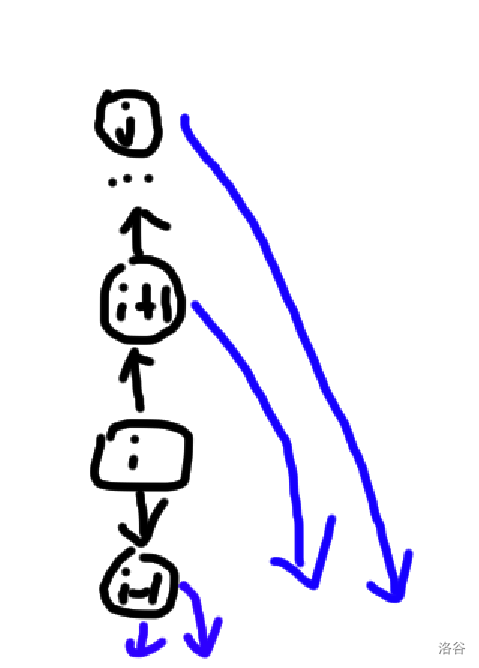
从点 开始,只有两种跳法:跳到 处,或者跳到 的因子 处. 跳到 处后等同于从 处开始,但跳到 和从 开始有一定区别,因为跳完后还可以往前跳(只要不超过 即可).

(上图黑线表示第一步、蓝线表示第二步,直线表示从 跳到 的类型,曲线从 跳到 的因子的类型.)
我们用 表示从 出发到 ,且经过的点在 范围内的方案数,我们要求的答案即为 . 根据前面的分析,可以得到:
那么对于 的 怎么求呢?首先根据定义 的方案对 有贡献.
如果我们要到达 点,必须是刚开始就从 向前跳到 ,到达 点后,不能再到 或者 ,只能跳到 的因子处离开,且这个因子必须小于 .
可以得到:
观察到我们推的两个式子形式相似,可以放在一个循环中,动态规划的边界即为 .
对于每个数,我们可以提前预处理因子,算法的时间复杂度为 ,优化一下常数,把对 取模改成减去 即可通过.
代码:
#include <iostream> #include <vector> const int MAXN = 5005; using namespace std; int n; long long f[MAXN][MAXN], mod; vector<int> d[MAXN]; int main() { cin >> n >> mod; for (int i = 1; i <= n; ++i) f[1][i] = 1; for (int i = 1; i <= n; ++i) { for (int j = 1; j * j <= i; ++j) { if (i % j == 0) { d[i].push_back(j); if (i / j != j) d[i].push_back(i / j); } } } for (int i = 2; i <= n; ++i) { f[i][i] = f[i - 1][i - 1]; for (int j = i; j <= n; ++j) { f[i][j] += f[i][j - 1]; for (int k : d[j]) { if (k < i) { f[i][j] += f[k][i - 1]; if (f[i][j] > mod) f[i][j] -= mod; } } } } cout << f[n][n] % mod << endl; return 0; }
信息
- ID
- 19
- 时间
- 2000ms
- 内存
- 512MiB
- 难度
- 6
- 标签
- 递交数
- 237
- 已通过
- 48
- 上传者