题目背景

「此情可待成追忆 只是当时已惘然」

题目描述

给定一棵大小为 $n$ 的有根树，点的编号 $1$ 到 $n$，根节点为 $1$ 号节点。

点 $i$ 有一个二元组 $(dep_i,str_i)$，其中 $dep_i$ 表示 $i$ 到根的距离，$str_i$ 表示从根节点到 $i$ 的简单路径上的所有节点的编号顺次连接组成的一个字符集为点的编号的字符串。

有 $q$ 次询问，每次询问给定 $x$ 和 $k$，请你输出 $f(x,k)$ 的值，$f(x,k)$ 的计算方式如下：

1. 求出 $(x,k)$ 邻域内的点的编号集合 $S$。

2. 将 $S$ 中的点按照其二元组升序排序（即以 $dep$ 为第一关键字，以 $str$ 的字典序为第二关键字从小到大排序），排序后的点记为 $c_1,c_2,\ldots,c_{|S|}$。

3. $f(x,k)$ 的值即为 $\sum_{i=1}^{|S|-1} \operatorname{Dis}(c_i,c_{i+1})$。

定义 $u$ 到 $v$ 的距离，即 $\operatorname{Dis}(u,v)$，为从 $u$ 到 $v$ 的树上唯一简单路径上的边数。

定义 $(u,d)$ 邻域表示树上与 $u$ 的距离 $\le d$ 的点集。

输入格式

第一行，两个整数 $n,q$，分别表示节点个数和询问个数。

第二行，$n-1$ 个整数，第 $i$ 个整数表示 $i+1$ 号节点的父亲 $p_{i+1}$。

接下来 $q$ 行，每行两个整数 $x,k$，表示一次询问。

输出格式

共 $q$ 行，每行一个整数表示对应询问的答案。

样例

10 3
1 2 2 3 4 5 6 6 9 
1 3
3 2
4 3

11
8
15

样例 1 解释

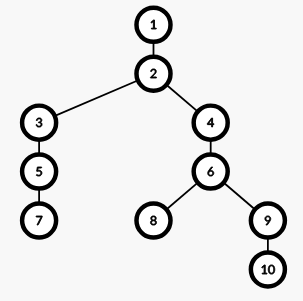
每个点的二元组如下所示（其中 $\mid$ 仅作为字符串中字符的区分方式）：

节点编号	二元组
$1$	$(0,1)$
$2$	$(1,1 \mid 2)$
$3$	$(2,1 \mid 2 \mid 3)$
$4$	$(2,1\mid 2\mid 4)$
$5$	$(3,1\mid 2\mid 3\mid 5)$
$6$	$(3,1 \mid 2 \mid 4 \mid 6)$
$7$	$(4,1\mid 2\mid 3\mid 5\mid 7)$
$8$	$(4,1\mid 2\mid 4\mid 6\mid 8)$
$9$	$(4,1\mid 2\mid 4\mid 6\mid 9)$
$10$	$(5,1\mid 2\mid 4\mid 6\mid 9\mid 10)$

对于第一组询问 $(1,3)$，其 $c$ 序列为 $1,2,3,4,5,6$，故 $f(1,3)=\operatorname{Dis}(1,2)+\operatorname{Dis}(2,3)+\operatorname{Dis}(3,4)+\operatorname{Dis}(4,5)+\operatorname{Dis}(5,6)=11$。

对于第二组询问 $(3,2)$，其 $c$ 序列为 $1,2,3,4,5,7$，故 $f(3,2)=8$。

对于第三组询问 $(4,3)$，其 $c$ 序列为 $1,2,3,4,5,6,8,9,10$，故 $f(4,3)=15$。

10 10
1 2 2 3 4 5 6 6 9 
1 3
3 2
4 3
10 3
2 2
3 3
5 3
1 0
7 2
1 2

11
8
15
5
11
16
8
0
2
4

数据范围

本题使用子任务捆绑。

对于所有的测试数据，满足 $1\le n,q\le 5\times 10^5$，$1\le p_i<i$，$1\le x\le n$，$0\le k\le n$。

子任务编号	$n,q\leq$	特殊性质	测试点分值
$1$	$1000$	无	$5$
$2$	$2\times 10^5$	A	$25$
$3$	$1\times 10^5$	B	$10$
$4$		无	$15$
$5$	$2\times 10^5$
$6$	$5\times 10^5$		$30$

• 特殊性质 A：保证每个点的父亲在合法范围内随机生成。
• 特殊性质 B：保证每个叶子节点的深度相同。

提示

请注意使用较快的输入输出方式。